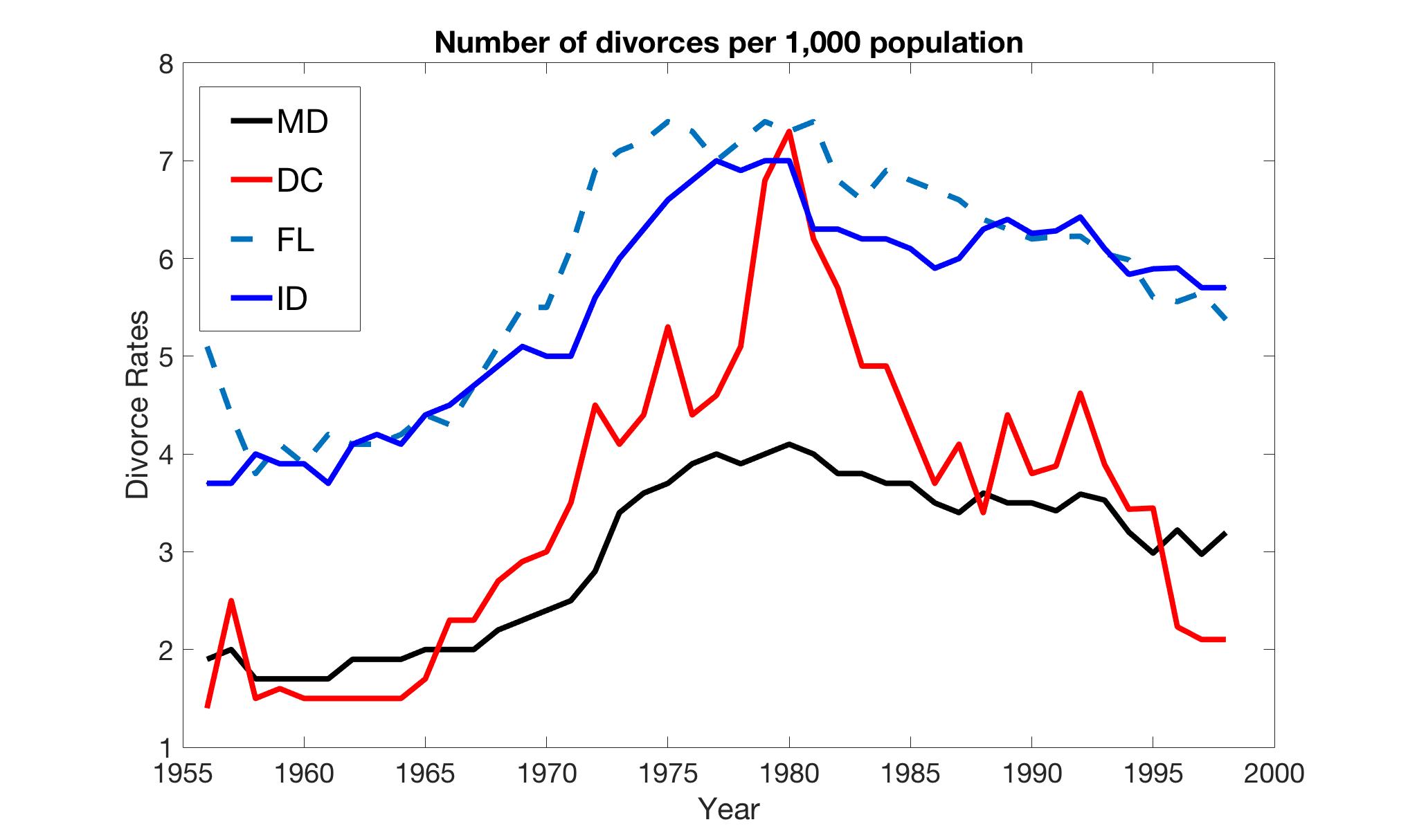
• Abstract: We consider efficient estimation of panel data models with interactive effects, which relies on a high- dimensional inverse covariance matrix estimator. By using a consistent estimator of the error covariance matrix, we can take into account both cross-sectional correlations and heteroskedasticity. In the presence of cross-sectional correlations, the proposed estimator eliminates the cross-sectional correlation bias, and is more efficient than the existing methods. The rate of convergence is also improved. In addition, we find that when the statistical inference involves estimating a high-dimensional inverse covariance matrix, the minimax convergence rate on large covariance estimations is not sufficient for inferences. To address this issue, a new ‘‘doubly weighted convergence’’ result is developed. The proposed method is applied to the US divorce rate data. We find that our more efficient estimator identifies the significant effects of divorce-law reforms on the divorce rate, and provides tighter confidence intervals than existing methods. This provides a confirmation for the empirical findings of Wolfers (2006) under more general unobserved heterogeneity.

• Paper: pdf file

• Previous version includes efficient estimation of factors: pdf file

• Matlab codes: beta_inter_effect, otherfunctions

• Real Data Study: matlab code , data from the website of Justin Wolfers

  

• Slides: pdf file

• Related literature:

  Fan, Liao and Mincheva (2012)
  Large covariance estimation by thresholding principal orthogonal components
  J. Roy. Statist. Soc. Ser. B (with discussion) (2013) 75, 603-680